Cómo Calcular el Centroide de un Triángulo: Guía Paso a Paso

¿Qué es el centroide de un triángulo?

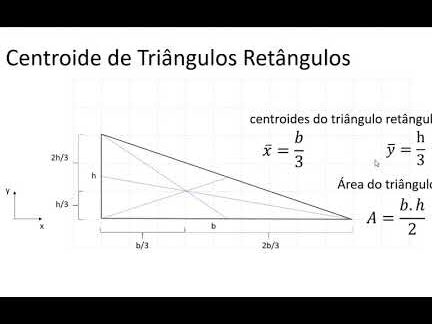
El centroide de un triángulo es el punto donde se intersectan las tres medianas del triángulo. Las medianas son los segmentos que conectan cada vértice del triángulo con el punto medio del lado opuesto. Este punto tiene propiedades únicas y es fundamental en la geometría, ya que se considera el "centro de masa" del triángulo.

Propiedades del centroide

• División de áreas: El centroide divide cada mediana en una proporción de 2:1, donde la parte más larga está más cerca del vértice.
• Coordenadas: Las coordenadas del centroide se pueden calcular como la media aritmética de las coordenadas de los vértices del triángulo.
• Simetría: En triángulos equiláteros, el centroide coincide con el ortocentro, el circuncentro y el baricentro.

La fórmula para determinar las coordenadas del centroide (G) de un triángulo con vértices en A(x1, y1), B(x2, y2) y C(x3, y3) es:

G(x, y) = (x1 + x2 + x3) / 3, (y1 + y2 + y3) / 3

Esta sencilla fórmula permite calcular el centroide de cualquier triángulo, independientemente de su forma o tamaño.

Cómo calcular el centroide de un triángulo: Fórmulas y ejemplos

El centroide de un triángulo, también conocido como el centro de gravedad, es el punto donde se intersectan las medianas del triángulo. Para calcular su posición, se pueden utilizar diferentes fórmulas según las coordenadas de los vértices del triángulo. La fórmula más común para encontrar el centroide (G) de un triángulo cuyas coordenadas de los vértices son (x1, y1), (x2, y2) y (x3, y3) es:

Fórmula del centroide

La fórmula para calcular el centroide es:

• Gx = (x1 + x2 + x3) / 3
• Gy = (y1 + y2 + y3) / 3

Donde Gx y Gy son las coordenadas del centroide. Este método es sencillo y efectivo para determinar la ubicación del centroide en un plano cartesiano.

Ejemplo práctico

Supongamos que tenemos un triángulo con los siguientes vértices:

• (2, 3)
• (4, 5)
• (6, 1)

Para calcular el centroide, aplicamos la fórmula:

• Gx = (2 + 4 + 6) / 3 = 4
• Gy = (3 + 5 + 1) / 3 = 3

Por lo tanto, el centroide del triángulo se encuentra en el punto (4, 3).

Propiedades del centroide de un triángulo que debes conocer

El centroide de un triángulo, también conocido como el punto de equilibrio, es el punto donde se intersectan las medianas del triángulo. Este punto tiene varias propiedades importantes que son fundamentales en geometría y aplicaciones prácticas. A continuación, se detallan algunas de estas propiedades:

1. Localización del centroide

• El centroide se encuentra a una distancia de 2/3 de cada mediana, contando desde el vértice hasta el punto medio del lado opuesto.
• La posición del centroide se puede calcular utilizando las coordenadas de los vértices del triángulo: (x, y) = ((x1 + x2 + x3) / 3, (y1 + y2 + y3) / 3).

2. Propiedades de equilibrio

• El centroide actúa como el punto de equilibrio del triángulo, lo que significa que si se coloca un triángulo sobre su centroide, se mantendrá en equilibrio.
• Este punto es crucial en aplicaciones de ingeniería y diseño, donde el equilibrio de fuerzas es esencial.

3. Relación con las áreas

• El área de un triángulo se puede dividir en tres subtriángulos, cada uno de los cuales tiene su propio centroide, y el centroide del triángulo original será el promedio de estos puntos.
• El centroide también se relaciona con la distribución de áreas en el triángulo, facilitando cálculos en geometría analítica.

Diferencias entre el centroide y otros puntos notables en un triángulo

El centroide de un triángulo, también conocido como el punto de intersección de las medianas, es un punto notable que se encuentra en el interior del triángulo. A diferencia de otros puntos notables como el circuncentro, incentro y ortocentro, el centroide tiene propiedades únicas que lo distinguen. Una de las principales diferencias es que el centroide divide cada mediana en una proporción de 2:1, donde la parte más larga está más cerca del vértice.

• Circuncentro: Es el punto donde se intersectan las mediatrices de los lados del triángulo y puede estar dentro, fuera o sobre el triángulo, dependiendo de su tipo (acutángulo, rectángulo u obtusángulo).
• Incentro: Es el punto donde se cruzan las bisectrices de los ángulos y siempre se encuentra dentro del triángulo, siendo el centro del círculo inscrito.
• Ortocentro: Este punto es donde se encuentran las alturas del triángulo y su ubicación varía; puede estar dentro, fuera o sobre el triángulo, dependiendo del tipo de triángulo.

Otra diferencia importante es que el centroide es el punto de equilibrio del triángulo, lo que significa que si se coloca el triángulo en un plano, el centroide es el punto donde se puede equilibrar. En cambio, los otros puntos notables no poseen esta propiedad de equilibrio, lo que los hace relevantes en diferentes contextos geométricos y físicos. Así, el centroide se asocia más con la geometría de masas, mientras que otros puntos notables tienen aplicaciones específicas en la construcción de triángulos y la resolución de problemas geométricos.

Aplicaciones del centroide de un triángulo en geometría y diseño

El centroide de un triángulo, también conocido como el centro de gravedad, es un punto fundamental en geometría que tiene diversas aplicaciones prácticas en el diseño y la ingeniería. Este punto se obtiene al intersectar las medianas del triángulo y se encuentra en la posición que equilibra el triángulo si se considera como un objeto plano uniforme.

[aib_post_related url='/apodo-para-tu-mejor-amigo-hombre/' title='Los Mejores Apodos para Tu Mejor Amigo Hombre: ¡Hazlo Sentir Especial!' relatedtext='Quizás también te interese:']

Aplicaciones en geometría

• Teoremas de equilibrio: El centroide es utilizado en teoremas que estudian el equilibrio de figuras geométricas, permitiendo calcular momentos y fuerzas en estructuras.
• División de áreas: En problemas de cálculo de áreas, el centroide ayuda a determinar el área efectiva de figuras compuestas.
• Transformaciones geométricas: Facilita el estudio de transformaciones y simetrías en triángulos, permitiendo obtener resultados más precisos.

[aib_post_related url='/diario-de-ana-frank-resumen-por-capitulos/' title='Diario de Ana Frank: Resumen Completo por Capítulos y Análisis Detallado' relatedtext='Quizás también te interese:']

Aplicaciones en diseño

• Arquitectura: En el diseño arquitectónico, el centroide se usa para crear estructuras que sean estéticamente agradables y estructuralmente eficientes.
• Diseño gráfico: En el diseño de logotipos y gráficos, el centroide ayuda a equilibrar los elementos visuales, logrando una composición armónica.
• Ingeniería mecánica: En la fabricación de componentes, se utiliza el centroide para optimizar la distribución de masa y mejorar la estabilidad de los productos.

La comprensión del centroide de un triángulo no solo es crucial para resolver problemas teóricos, sino que también tiene un impacto significativo en la práctica profesional en diversas disciplinas.

Te gusto este articulo? Cómo Calcular el Centroide de un Triángulo: Guía Paso a Paso puedes ver mucho mas aqui Noticias.